Prévoir les consommations électriques grâce à PAST
Le groupe SNCF a des besoins variés en termes de prédictions, comme par exemple pour la maintenance prédictive. Dans le cadre de l’achat d’électricité pour les trains, plusieurs approches de modélisation statistique ont été étudiées pour prévoir les consommations électriques à l’avance. Retrouvez l’expertise de la Factory Data & IA d'ITNOVEM.
Publié le 4 octobre 2021 par Com itnovem

La Factory Data & IA d’ITNOVEM, offre ses services d’expertise Big Data & IA face aux problématiques rencontrées dans le Groupe. Les prestations réalisées peuvent, par exemple, être des études de faisabilité de solutions data science délivrant des POC (1) (Proof Of Concept) ou des créations d’applications métiers en production répondant aux besoins des clients (maintenance prédictive, prédiction…).
Il y a de plus en plus de besoins en termes de prédiction, comme la prévision des retards des trains, la prédiction de leur consommation électrique ou encore l’anticipation de leurs pannes. Dans ces contextes, les données s’inscrivent dans le temps. Leur historique et leur état actuel (retard, consommation électrique et état de santé respectivement aux exemples listés précédemment) sont connus. Leur état futur est à prédire et est au cœur des enjeux du Groupe pour assurer un meilleur service, plus performant et plus fiable. De telles données sont souvent modélisables au moyen de séries temporelles (2). Nous avons donc initié un projet interne de recherche appliquée afin de s’approprier l’état de l’art académique concernant leurs modélisations et leurs prédictions. Les résultats de ce projet de recherche et les compétences que nous avons acquises viennent renforcer notre valeur ajoutée vis-à-vis de nos clients et du Groupe.
Cette initiative de montée en compétence s’inscrit dans un projet client, ENF (Energy Need Forecast) (3), pour la filiale SNCF Energie qui a pour mission de transmettre les ordres d’achat d’électricité pour différents clients en avance mais également les achats/reventes du jour pour le lendemain. Optimiser ses prévisions lui permet d’optimiser le coût de la fourniture d’électricité de traction. Pour cette raison la filiale dispose des modèles (métiers actuellement) de prédiction de consommation électrique. Nous avons exploité des données dont SNCF Energie dispose. Dans cette étude, nous nous sommes limités à la prédiction des jours que nous qualifierons de normaux, c’est à dire tous les jours hors grève. Les grèves sont en effet jugées peu prévisibles, aussi bien par leur impact que par leur occurrence, même pour un modèle de prédiction. Nous avons travaillé sur les données de consommation électrique des trains de l’activité SNCF Mobilités entre janvier 2014 et novembre 2019 au pas demi horaire. Pour des raisons de confidentialité nous ne présentons pas de comparaison entre les performances de modèles métier et celles des modèles étudiés.
Nettoyage des données et modélisation des variables
Nous avons commencé par nettoyer les données en deux étapes. Les jours de grève ont premièrement été retirés, car écartés du périmètre de l’étude. Le nouveau jeu de données a donc des trous temporels correspondant aux grèves sur la période considérée. Par exemple, il y a eu 2 jours de grève les 3 et 4 avril 2018. Le nouveau jeu de données n’a donc plus d’information sur ces 2 jours. La consommation du 2 avril à 23h30 est suivie par la consommation du 5 avril à 00h00. C’est ce saut temporel, différent de la période d’observation de 30 minutes, que nous appelons trou. Pour certains modèles la présence d’un trou dans les données n’est pas problématique. Cependant, pour d’autres modèles (par exemple le modèle ARMA (4) détaillé plus bas), il est nécessaire d’avoir des observations relevées à fréquence constante. Dans notre cas, cette fréquence correspond à une mesure toutes les 30 minutes. Pour étudier les performances des deux catégories de modèles, ceux ne nécessitant pas une fréquence d’observation constante et ceux le nécessitant, nous avons donc considéré deux jeux de données.
- Le premier jeu de données, troué, comprend les consommations de SNCF Mobilités sans les jours de grèves.
- Dans le second jeu de données où il est nécessaire d’avoir un historique de consommations échantillonnées à fréquence constante, les trous ont été remplacés par des consommations normales (hors grève). Nous avons, pour cela, construit un modèle d’ensemble d’arbres de décision construit par la méthode du gradient boosting (5). Ce modèle (entraîné exclusivement sur des jours normaux avec une méthode de validation croisée adaptée aux séries temporelles) nous a permis de remplacer les consommations des jours de grèves par des consommations normales simulées. Les variables explicatives retenues pour ce modèle sont les mêmes que celles utilisées pour les autres modèles et détaillés ultérieurement.
Une fois les données nettoyées, une étape de transformation de celles-ci en des paramètres pour les modèles, appelés features (6), a été réalisée. C’est le feature engineering (7). En fonction des propriétés des variables (booléennes, cycliques, catégorielles…), différentes méthodes sont implémentables.
Les variables catégorielles (8) non hiérarchisables peuvent être transformées en dummy variables (9). Pour chacune des catégories possibles de la variable d’origine, une feature est créée prenant comme valeur 1 ou 0 en fonction de la valeur de la variable d’origine. C’est le one-hot encoding (10). Par exemple pour une variable détaillant la catégorie du wagon, plusieurs features sont créées, autant que le nombre de catégories. Pour un wagon de catégorie « R12” la nouvelle feature associée à la catégorie “R12” sera à 1 et toutes les autres features créées seront à 0 (Tableau 1). Cette méthode est efficace lorsque la variable d’origine a un nombre modéré de valeurs différentes sinon beaucoup de nouvelles features sont créées avec beaucoup de 0.
| Variable d’origine | Features créées | |||
| Code_CR | Code_CR_R12 | Code_CR_R39 | Code_CR_K12 | … |
| R12 | 1 | 0 | 0 | 0 |
| R12 | 1 | 0 | 0 | 0 |
| R39 | 0 | 1 | 0 | 0 |
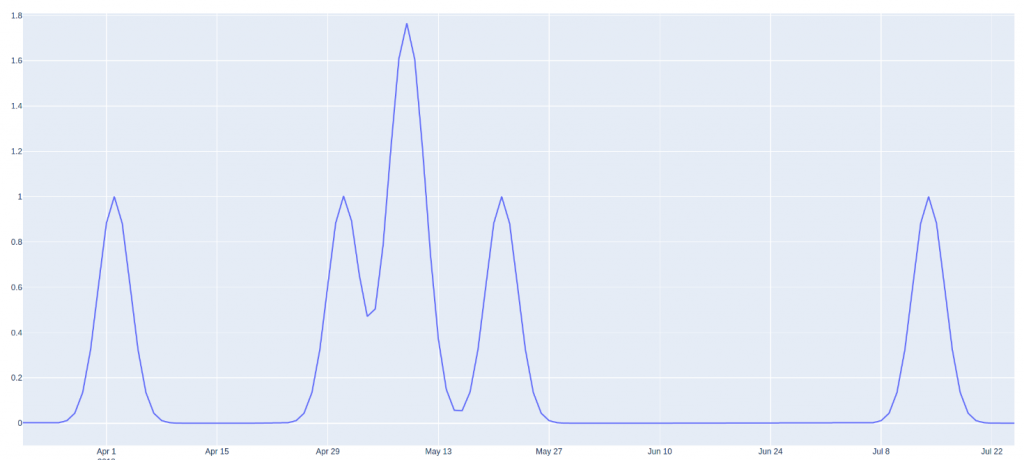
Les variables booléennes (11) (seulement deux valeurs possibles) peuvent être gardées telles quelles ou être transformées au moyen de la méthode des noyaux gaussiens (12) qui consiste à appliquer un noyau gaussien autour de chaque élément de la population prenant la valeur vraie. Cette méthode permet de propager l’effet sur les éléments proches temporellement. Le cumul de ces gaussiennes conduit à la construction d’une nouvelle feature. En appliquant cette astuce par exemple à la variable « jour férié », la nouvelle feature modélise la proximité (à un certain degré) du jour en question aux jours fériés, avant ou après, contrairement à une valeur booléenne incapable de modéliser cette information. En revanche, cette astuce de feature engineering nécessite l’ajustement d’un hyper paramètre : la ”fenêtre” (13) du noyau gaussien. Dans l’exemple ci-dessous, la variable « jour férié », booléen valant 0 ou 1 initialement, a été remplacée par une feature prenant des valeurs entre 0 et 2 modélisant la proximité à des jours fériés. Un jour en juin aura une valeur proche de 0. A l’inverse un jour en mai peut avoir une valeur supérieure à 1 s’il est proche de plusieurs jours fériés. Un jour proche d’un seul jour férié (veille ou lendemain par exemple) aura une valeur intermédiaire.
Les variables cycliques (qui prennent des valeurs périodiques) peuvent être modélisées de plusieurs façons. Garder ces variables intactes est problématique. Considérons l’exemple du jour de la semaine, qui est cyclique puisqu’il prend des valeurs de 1 (lundi) à 7 (dimanche) puis repasse à 1. L’inconvénient d’utiliser une telle variable dans sa forme numérique brute est que cela ne permet pas au modèle de prédiction de comprendre que le lundi (1) est proche du dimanche (7). Pour y remédier, deux méthodes de feature engineering peuvent être utilisées. Il est possible d’utiliser le noyau gaussien pour calculer une nouvelle feature. Dans notre exemple, une feature par jour sera créée. La feature du lundi vaut 1 sur les lundis et d’autres valeurs plus petites pour mardi et dimanche et encore plus petites pour les autres jours. Cette méthode est moins adaptée aux variables cycliques qui prennent des valeurs très variées comme le jour de l’année puisqu’elle va générer un grand nombre de features. Dans ces cas où la cardinalité de la variable est élevée, on place chaque valeur de la variable numérique sur un cercle unité de telle sorte que la valeur la plus faible de cette variable apparaisse juste à côté de celle la plus élevée. Nous calculons les composantes à l’aide des fonctions trigonométriques sinus et cosinus. En pratique cela revient à créer deux features par variable cyclique x en calculant : cos(2*pi*x/période) et sin(2*pi*x/période).
En synthèse, dans le cadre de ce projet, les variables utilisées ainsi que les méthodes de feature engineering sont détaillées dans le tableau ci-dessous.
| Variable | Type | Méthode appliquée |
| Jour férié | Booléenne | Astuce du noyau gaussien |
| Jour de grève | Astuce du noyau gaussien | |
| Jour de vacances | Dummy variable | |
| Jour du mois | Cyclique | Astuce cosinus/sinus |
| Jour de l’année | Astuce cosinus/sinus | |
| Semaine de l’année | Astuce cosinus/sinus | |
| Mois | Astuce du noyau gaussien | |
| Jour de semaine | Astuce du noyau gaussien | |
| Prévision température | Numérique | Inchangée |
Modèles statistiques étudiés
Une fois les features créées, plusieurs modèles de machine learning (14) (ML) ont été étudiés. Comme expliqué précédemment, il existe des modèles de prédiction adaptés aux séries temporelles et d’autres basés sur des approches statistiques classiques. Dans le cadre des modèles adaptés aux séries temporelles, le jeu de données avec les trous remplacés par des consommations normales simulées a été utilisé. L’un des modèles le plus utilisé est le modèle SARIMAX, extension du modèle ARMA (4), que nous avons étudié dans le cadre de notre projet. Décomposons l’acronyme :
- Seasonal (S), pour modéliser la saisonnalité.
- Auto Regressive (AR), Les modèles AR prédisent la valeur suivante de la série temporelle étudiée grâce à une combinaison linéaire des observations précédentes.
- Integrated (I), modéliser la tendance.
- Moving Average (MA), Les modèles MA prédisent la valeur suivante grâce à une combinaison linéaire des termes stochastiques précédents (modélisés par un bruit blanc).
- eXogenous (X), le caractère exogène modélise une combinaison linéaire de variables exogènes (différentes de la série temporelle d’étude). Par exemple, dans le cas étudié lors de ce projet, la série temporelle est la consommation et les variables exogènes ajoutées au modèle ont été les températures prévisionnelles et l’information jour férié ou non.
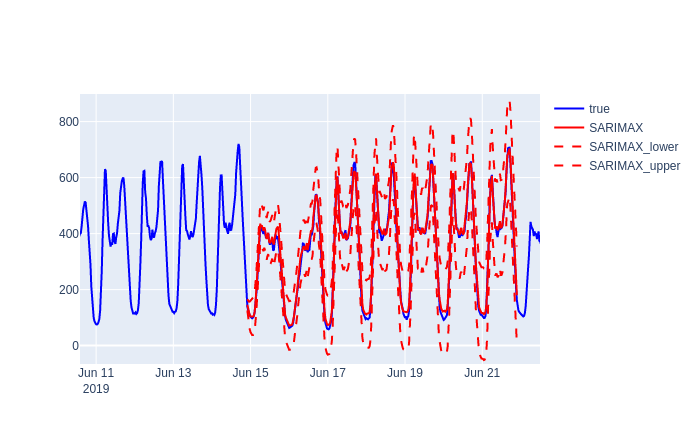
Les modèles ARMA sont des modèles combinant la composant AR et MA. Les modèles SARIMA sont des cas particuliers des modèles ARMA pour modéliser une saisonnalité ou une tendance grâce aux termes S et I. Ces modèles modélisent des variables aléatoires et permettent donc nativement d’obtenir des intervalles de confiance pour les prédictions. Voici un exemple de prédiction d’un modèle ARMA après décomposition saisonnière de la consommation initiale. La courbe bleue est la consommation observée. La courbe rouge continue est la moyenne de la prédiction. Les courbes rouges en traitillées sont les prédictions de la moyenne plus ou moins deux écarts types, ce qui correspond à un intervalle de confiance à 95 % dans le cas où le bruit est normalement distribué.
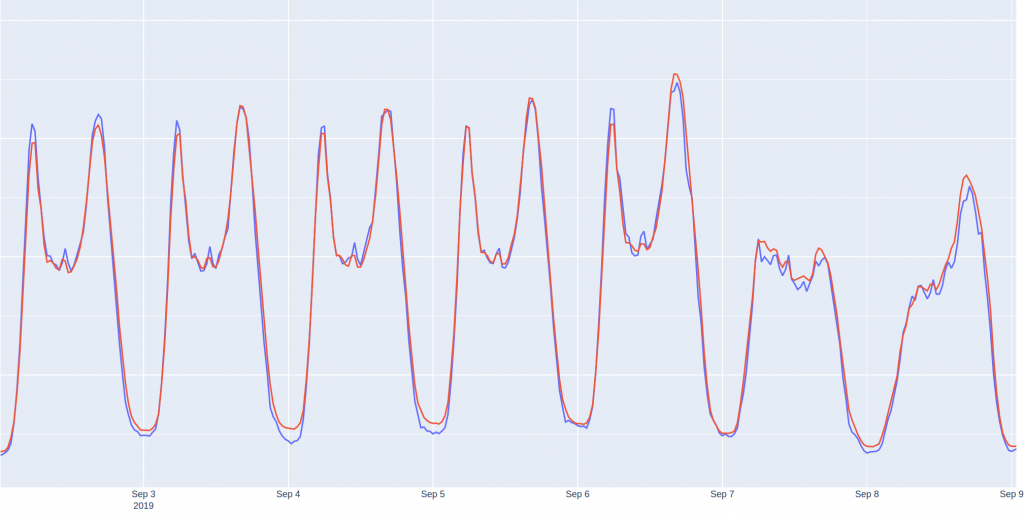
Il est également possible de formuler un problème de prédiction de série temporelle en un modèle de machine learning supervisé de régression où la cible est la valeur de l’instant à prédire. Le jeu de données avec des trous est dans ce cas utilisé. En plus des features listées précédemment, des valeurs de la consommation dans le passé par rapport à l’instant à prédire sont ajoutées. Ces intervalles capturent le caractère autorégressif de la série temporelle, qui n’est pas naturellement détecté par cette catégorie de modèle, contrairement aux modèles dédiés aux séries temporelles. Par exemple, la valeur de la journée d’avant, puis de la semaine d’avant puis de deux semaines avant sont de bons choix. En effet la consommation d’un vendredi à 7h30 sera probablement similaire à la consommation du vendredi de la semaine précédente à 7h30, par contre elle n’aura probablement aucune corrélation avec la consommation de dimanche 13h30 de la semaine passée. Cette étape reste très importante pour la construction d’un bon modèle. Une méthode assez simple pour la sélection de ces délais est de tracer la courbe d’auto corrélation de la série et de choisir les intervalles où des pics sont observés. Un fois ces nouvelles features ajoutées, nous avons étudié plusieurs modèles de ML, que nous appelons modèles génériques puisque non propre aux séries temporelles. Entre autres, nous avons utilisé un modèle de prédiction basé sur un ensemble d’arbres de décision (15) construit par la méthode du gradient boosting (comme introduit mais non détaillé plus haut). Ce modèle présente plusieurs avantages. Il permet de modéliser les non-linéarités entre les features et la cible (contrairement à la régression linéaire par exemple). Il est relativement interprétable et compréhensible (comparativement aux modèles deep learning). Il est très performant puisque les arbres de décision sont construits itérativement pour corriger les erreurs du modèle. Ainsi lorsque 3 arbres ont été construits, le 4ème arbre de décision est construit pour corriger les erreurs de l’ensemble des 3 premiers arbres.
Enfin, un troisième modèle a été testé. Il s’agit d’un réseau de neurones récurrents (16) (RNN), modèle deep learning (17), qui modélise des séries temporelles et nécessite donc d’utiliser le jeu de données avec les trous remplacées par des consommations simulées. Dans le cas général, il prend en entrée une séquence de données ( , , … ) où les sont des vecteurs au lieu d’une seule donnée à la fois comme c’est le cas pour les réseaux de neurones classiques. Ainsi un RNN apprend à prédire une valeur cible non seulement en utilisant les features de l’élément mais aussi sa position dans la séquence et sa relation avec les éléments amont (et éventuellement avals pour certains modèles) dans la séquence. Les RNNs permettent de modéliser le caractère autorégressif des données séquentielles comme le texte et les séries temporelles.
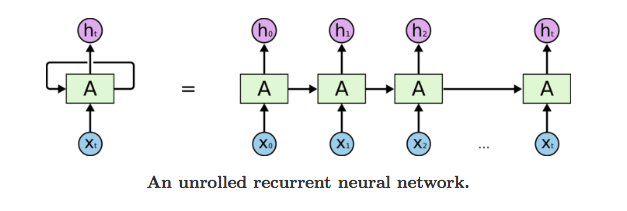
Source : https://towardsdatascience.com/understanding-rnn-and-lstm-f7cdf6dfc14e
Dans le cadre de notre étude, la série de temporelle de consommation électrique au pas demi-horaire est décomposée en plusieurs séquences en utilisant une fenêtre glissante à taille fixe (par exemple 30 jours). Chaque séquence en entrée correspond à une liste de vecteurs avec une seule feature (la consommation électrique) et comme valeur cible la consommation de la demi-heure suivante. Il est aussi possible de connecter la sortie du RNN à un réseau de neurones dense afin d’intégrer les autres features de l’instant cible. L’architecture utilisée durant l’étude est la suivante :
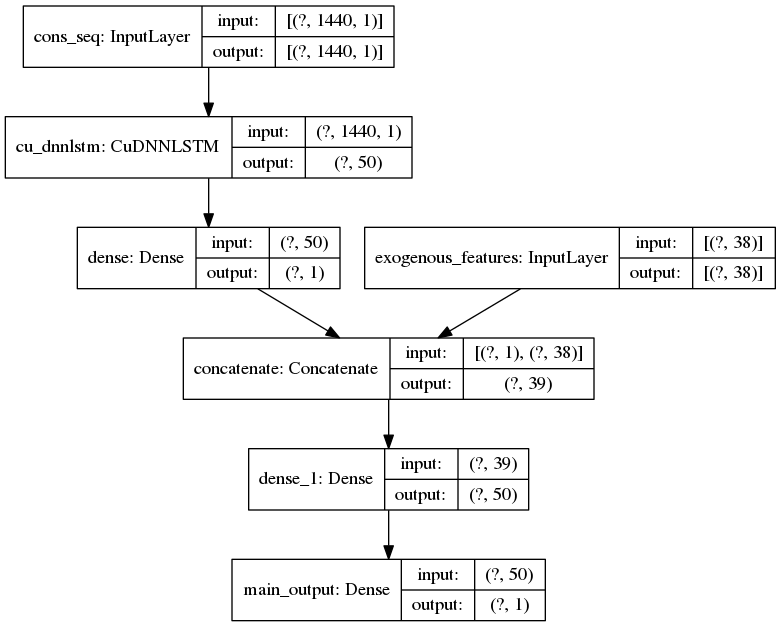
Selon la quantité de données, la taille d’un réseau de neurones et le nombre d’itérations retenues, l’entraînement peut durer assez longtemps surtout sous CPU. Durant l’étude, il a été réalisé sous GPU pour presque 15 fois moins de temps que sous CPU.
Conclusion
Dans le cadre de ce projet interne mené au sein de la Factory Data & IA d’ITNOVEM, filiale technologique du groupe SNCF, nous avons renforcé nos compétences autour de la modélisation et de la prédiction de séries temporelles. Dans le cas des données étudiées dans ce projet, nous sommes parvenus à obtenir des scores comparables à ceux du modèle métier en production. Dans le contexte spécifique de notre client, ces modèles apportent en plus la possibilité d’automatiser les opérations de prévisions de consommations, réalisées quotidiennement. De tels modèles pourraient également apprendre les évolutions de comportement des axes au cours du temps. Ces méthodes et résultats peuvent bénéficier aux différents acteurs métier du Groupe. C’est la raison pour laquelle nous avons déjà partagé avec la filiale SNCF Energie nos résultats et entamé des discussions pour une possible industrialisation de l’une de ces approches innovantes.
Si ces travaux vous ont donné des idées ou levé des questions sur vos problématiques métier, n’hésitez pas à prendre contact avec la Factory Data & IA.
Auteurs
- CAPITAINE Arnaud, Data Scientist
- INTRONATI Guido, Lead Data Scientist
- NONNE Héloïse, Head of Data Science and Engineering
- SOUIKI Amine, Data Scientist
| Références 1. Preuve de concept. wikipedia. [En ligne] https://fr.wikipedia.org/wiki/Preuve_de_concept. 2. Série temporelle. wikipedia. [En ligne] https://fr.wikipedia.org/wiki/S%C3%A9rie_temporelle. 3. Prédire la consommation électrique des trains avec Energy Need Forecast. digital.sncf. [En ligne] 25 11 2019. https://www.digital.sncf.com/actualites/predire-la-consommation-electrique-des-trains-avec-energy-need-forecast. 4. ARMA. wikipedia. [En ligne] https://fr.wikipedia.org/wiki/ARMA. 5. Gradient boosting. wikipedia. [En ligne] https://en.wikipedia.org/wiki/Gradient_boosting. 6. Feature (machine learning). wikipedia. [En ligne] https://en.wikipedia.org/wiki/Feature_(machine_learning). 7. Feature engineering. wikipedia. [En ligne] https://en.wikipedia.org/wiki/Feature_engineering. 8. Variable catégorielle. wikipedia. [En ligne] https://fr.wikipedia.org/wiki/Variable_cat%C3%A9gorielle. 9. Dummy variable (statistics). wikipedia. [En ligne] https://en.wikipedia.org/wiki/Dummy_variable_(statistics). 10. Encodage one-hot. wikipedia. [En ligne] https://fr.wikipedia.org/wiki/Encodage_one-hot. 11. Booléen. wikipedia. [En ligne] https://fr.wikipedia.org/wiki/Bool%C3%A9en. 12. Vincent Warmerdam: Winning with Simple, even Linear, Models | PyData London 2018. youtube. [En ligne] 27 05 2018. https://www.youtube.com/watch?v=68ABAU_V8qI. 13. Estimation par noyau. wikipedia. [En ligne] https://fr.wikipedia.org/wiki/Estimation_par_noyau. 14. Apprentissage automatique. wikipedia. [En ligne] https://fr.wikipedia.org/wiki/Apprentissage_automatique. 15. Arbre de décision. wikipedia. [En ligne] https://fr.wikipedia.org/wiki/Arbre_de_d%C3%A9cision. 16. Réseau de neurones récurrents. wikipedia. [En ligne] https://fr.wikipedia.org/wiki/R%C3%A9seau_de_neurones_r%C3%A9currents. 17. Apprentissage profond. wikipedia. [En ligne] https://fr.wikipedia.org/wiki/Apprentissage_profond. 18. Feature Engineering – Handling Cyclical Features. blog.davidkaleko. [En ligne] 30 10 2017. http://blog.davidkaleko.com/feature-engineering-cyclical-features.html. 19. Réseau de neurones récurrents. wikipediaa. [En ligne] https://fr.wikipedia.org/wiki/R%C3%A9seau_de_neurones_r%C3%A9currents. |